修士論文｜雲粒数濃度の違いによる台風の強度・構造に対する感度実験

Introduction

台風は様々な災害をもたらす大気現象

　台風は様々な災害をもたらす大気現象であり，過去にも日本で被害がもたらされた。また，温暖化による台風の激甚化も予想されており，台風被害を低減することが社会全体における課題となっている。現在，この課題に対し，台風の長期的な強度を抑制する方法が検討されている。その一つに，台風を構成する雲に凝結核として働くエアロゾルを散布する方法がある。

雲の構造は雲粒の数に依存

　雲は雲粒や氷粒子が集まって形成されている。水滴が形成される過程では，エアロゾルが凝結核（Cloud Condensation Nuclei: CCN）となり，その周りに水蒸気が凝結することで，水滴が形成される。また，凝結核の数に応じて，雲を構成する粒である雲粒の数も変わり，雲全体の形状や性質を変えると考えられている（図1，Twomey 1977; Rosenfeld et al. 2008）。さらに台風では，中心付近で水蒸気が凝結する分布が変わると，台風自体の構造が変わることから，凝結核の数が変化すると台風の強度も変化すると考えられている（図2）。しかしながら，雲粒数の違いと台風強度との関係は複雑で，十分な検証がなされていないのが現状である。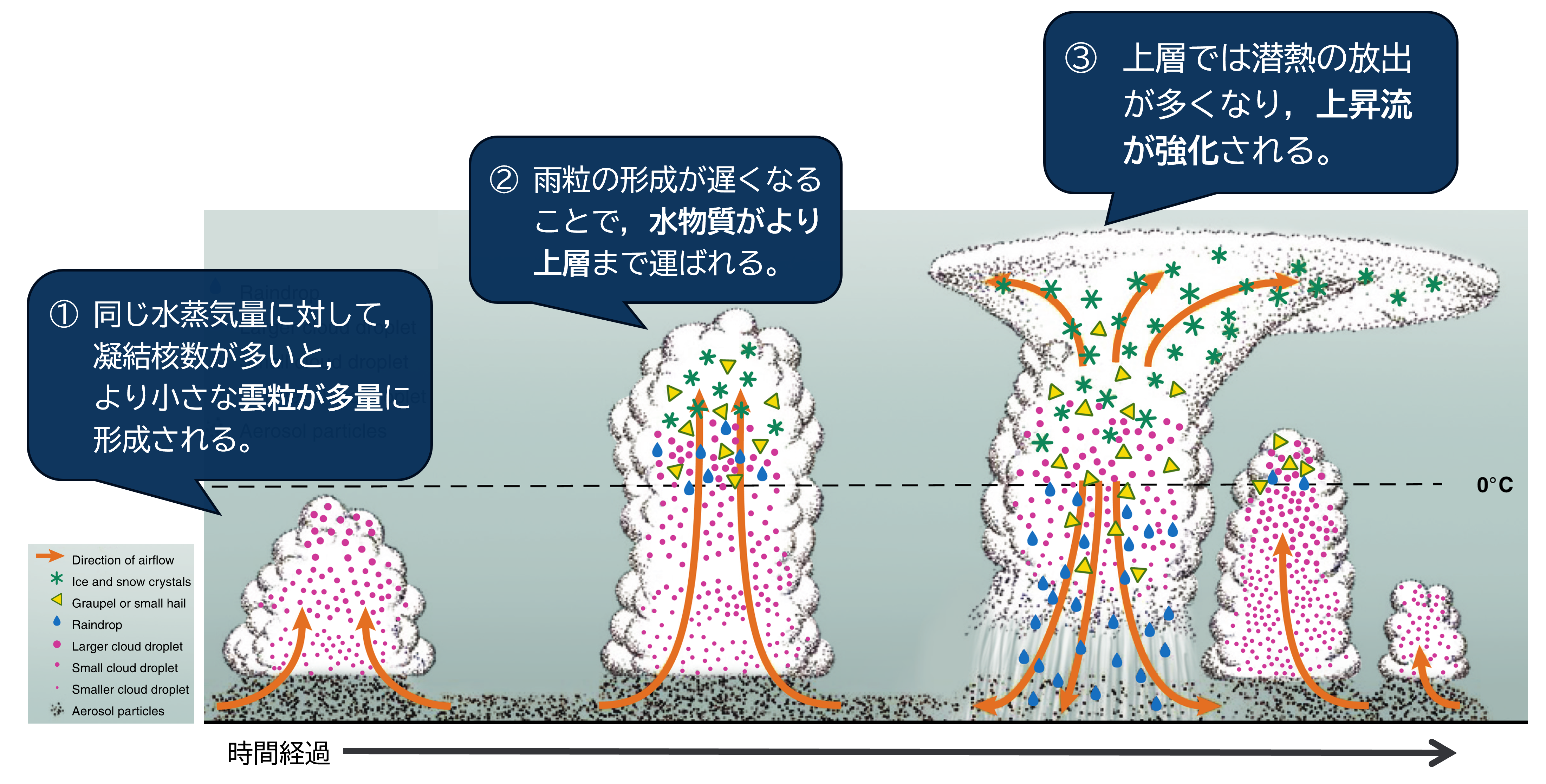

▲図1：雲粒数が多いときの積乱雲の発達過程。Rosenfeld et al.(2008)に一部加筆。

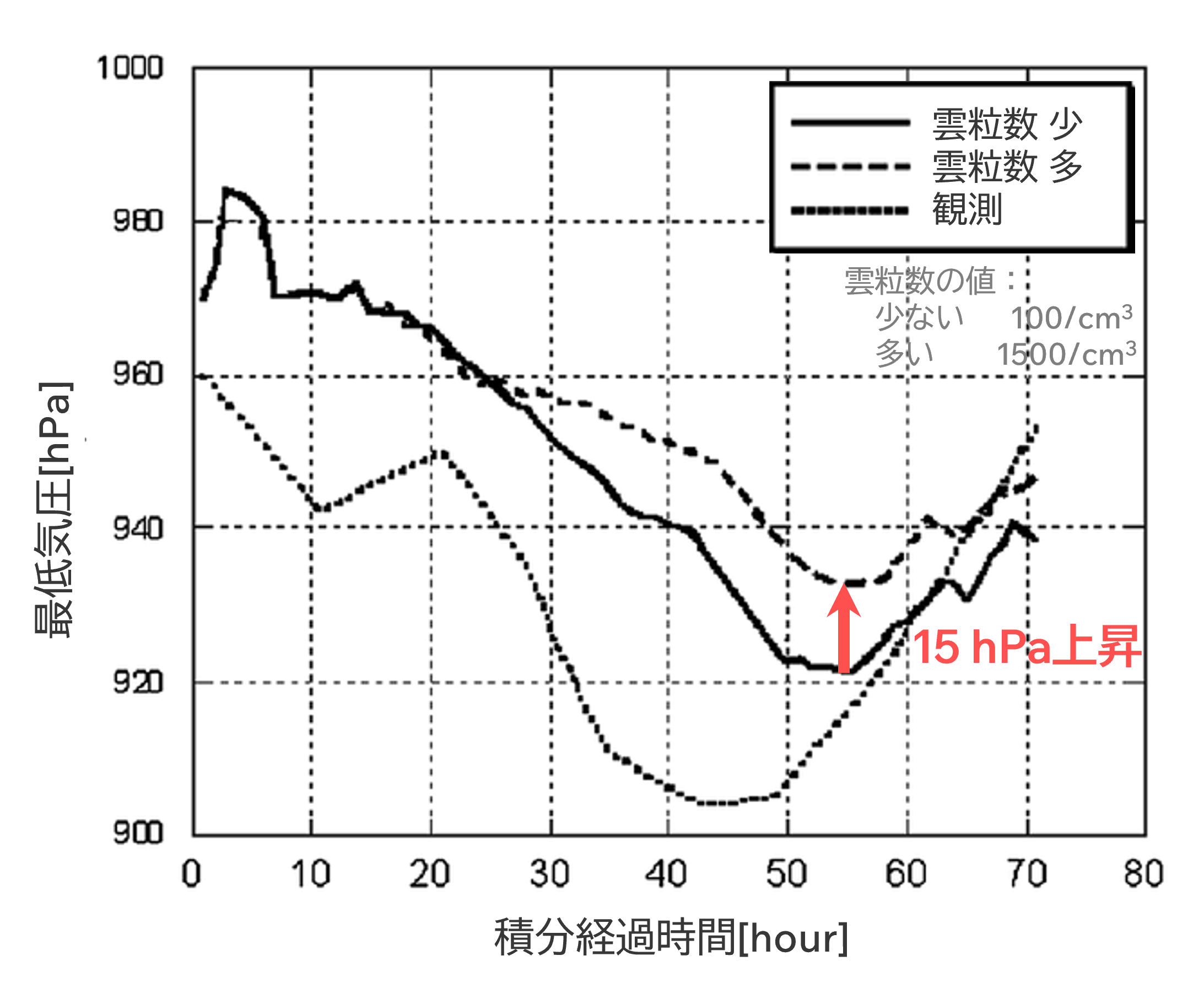
▲図2：雲粒の量の変更させたハリケーンKatrinaの最低気圧の時系列。Khain et al.(2010)に一部加筆。
　

研究目的

　本研究では，雲粒数の増減が台風強度を表す指標の一つである中心気圧に及ぼす影響を評価することを目的とした。本目的を果たすため，複数の台風事例を対象した雲粒数を変化させる理想化された感度実験を実施した。

Method

シミュレーション対象とする台風の選定

選定手順

対象とした台風

2018年台風第21号(Jebi)
2018年台風第24号(Trami)
2019年台風第19号(Hagibis)
2019年台風第21号(Bualoi)
2021年台風第16号(Mindulle)
2022年台風第14号(Nanmadol)

シミュレーションの概要

使用モデル

　CReSS-4ICE-CCN（Tsuboki 2008; 村上ほか 2021）

共通のシミュレーション設定

　表1に6事例で共通するシミュレーション設定を示す。水平解像度は0.03°（約3 km）とし，鉛直層数は60層のストレッチング座標系を採用し，平均鉛直距離は360 mとなっている。海面水温（Sea Surface Temperature; SST）には，気象庁の高解像度海面水温データMGDSST（水平解像度0.25度）を使用した。なお，海面水温は初期時刻における海面水温データで固定させた。初期値に気象庁GSMデータを使用し，6時間ごとに境界値を与えた。雲微物理モデルにはダブルモーメントバルク法を用いた。サブグリッドスケールの乱流には1.5次のクロージャーモデルを用いた。タイムスリップは4秒とし，600秒ごとに計算結果を出力させて，それぞれ36時間のシミュレーションを実施した。

表1　シミュレーションで共通の設定。
項目	設定
格子間隔	dx = dy = 0.03°（約3 km）
鉛直層数	60
積分時間	36時間
物理過程	雲物理過程：NHM-4ICE 乱流過程　：1.5-order TKE 地表面過程：バルク法
初期値・境界値	JMA GSM

計算領域

　図3に計算領域，初期時刻，格子点数を示す。計算領域は境界からの影響をなるべく少なくするために，擾乱が境界から500 km以上離れるように設定した。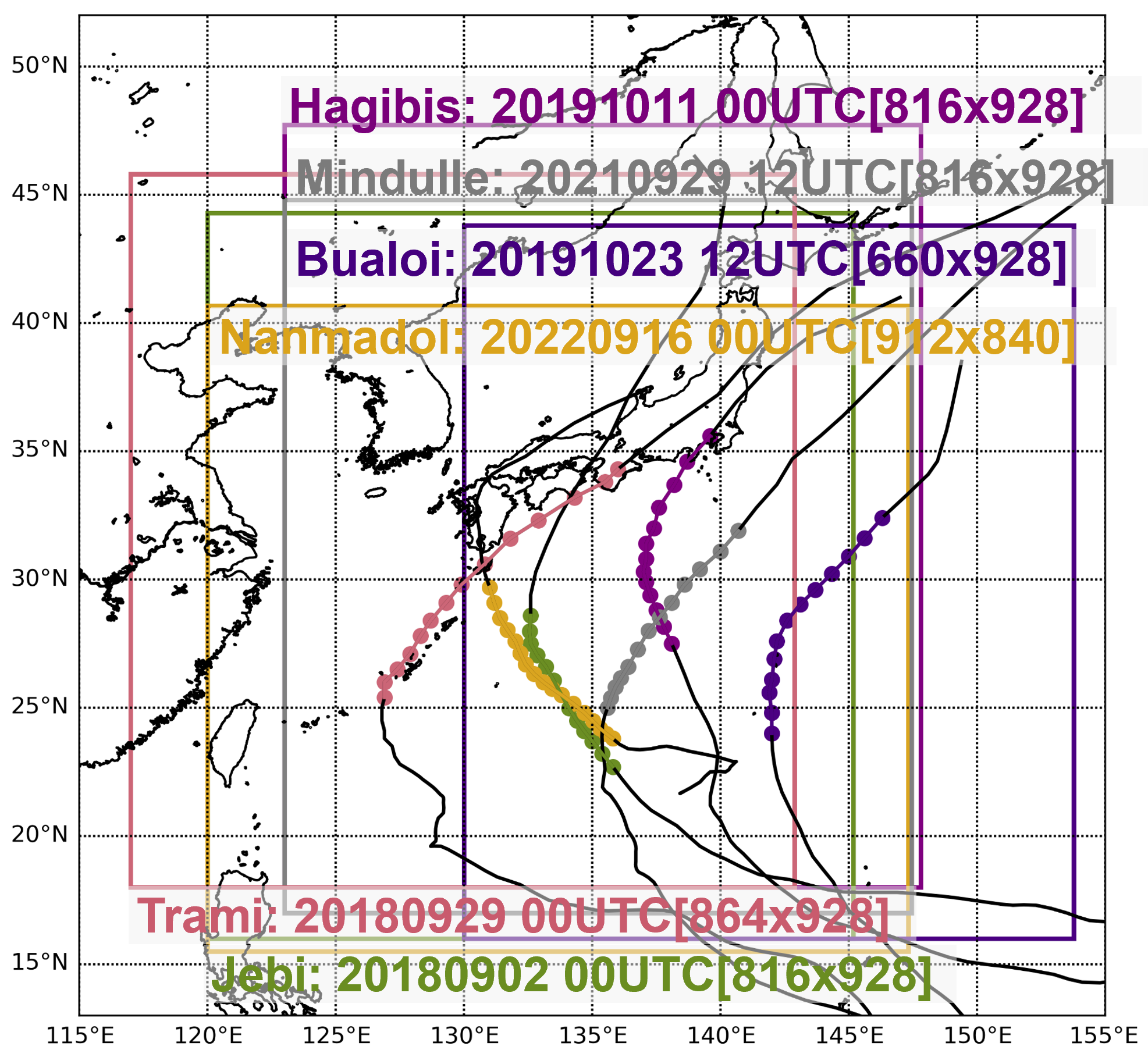

▲図3：台風の経路(計算期間は色付け)と計算領域，初期時刻[格子点数]。
　

感度実験方法

　雲凝結核スペクトルのパラメータを変更する方法により実施した。雲粒の数\(N_{CCN}\)を求める近似式（これを雲凝結核スペクトルという，Twomey et al. 1959）は式(1)で表される。
\[ N_{CCN} = C \cdot SS_w ^ k \tag{1} \] ここで，\(SS_w\)は過飽和度，\(C\)は過飽和度1%における雲凝結核数濃度を表し，\(k=0.63\)である。本研究では，過飽和度1%における雲凝結核数濃度を表す\(C\)の値を表2のとおりに設定し，計算領域全体で一様と仮定してシミュレーションを実施した。CTLが日本域の強風が吹く環境下において標準とされる値に近しい設定であり，台風6事例それぞれでCTLにて設定された300に対し1桁ずつの幅で増減させたシミュレーションとなっている。なお，この値はそれぞれの台風事例におけるエアロゾル数濃度を表しているわけではない。

表2　変更させた定数\(C\)の値。
\(C\)の値 \(\mathrm{[cm^3]}\)	30 Clean	300 CTL	3000 Polluted

　上記の設定でシミュレーションされた台風の積分期間および方位角に平均した雲粒数の半径高度断面の一例を図4に示す。雲粒数がCTLに対し，Cleanでは減少し，Pollutedでは増加したことが確認できることから，モデル内での雲粒の数を正しく変更させることができていると判断した。

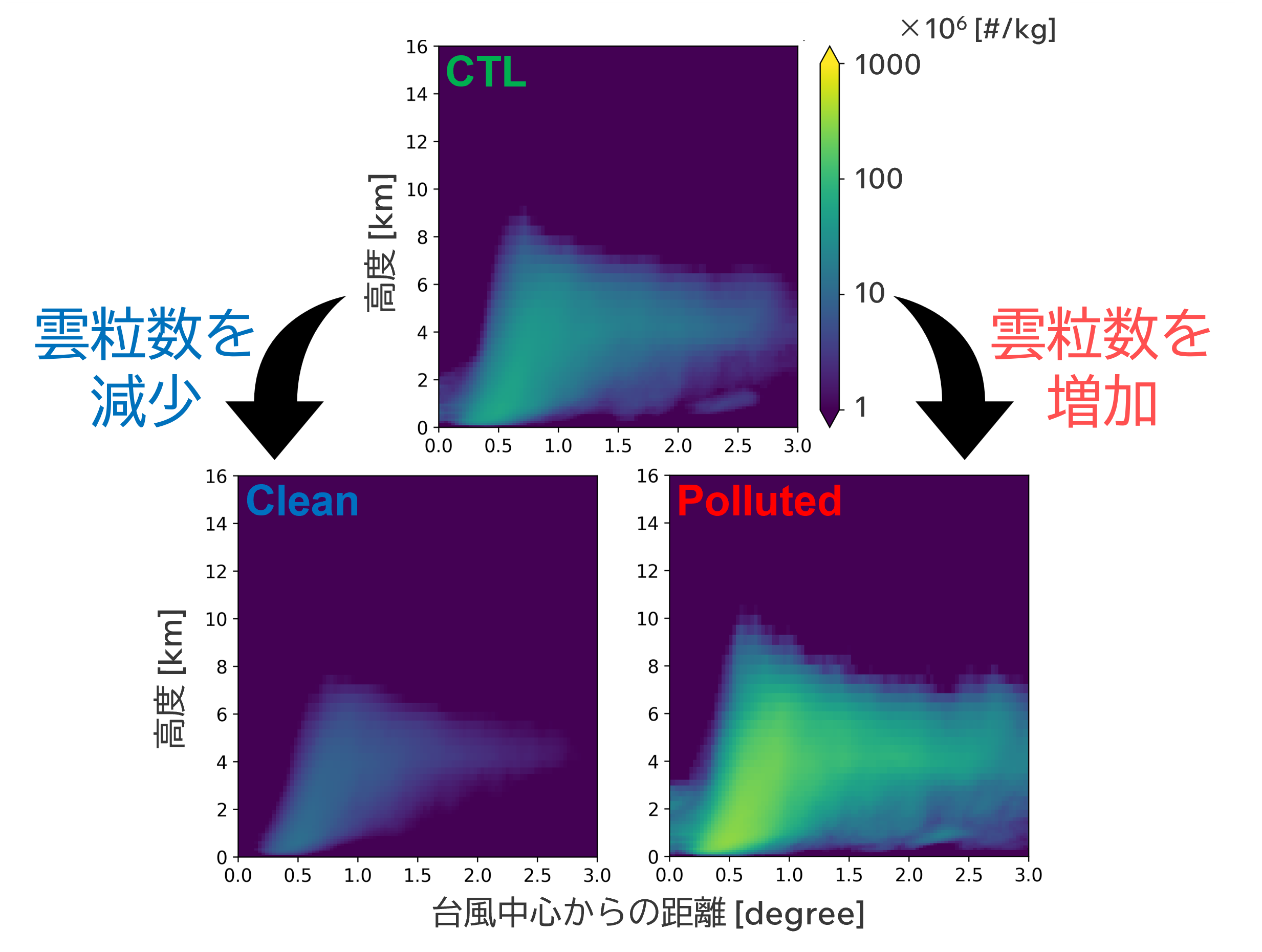
▲図4：Bualoi事例における積分期間および方位角に平均した雲粒数の半径高度断面。
　

Result

雲粒数の増減による中心気圧の時系列変化

　図5にCTL実験を基準として中心気圧の差分を計算して時系列変化の影響を除いた気圧変化量を示す。雲粒数を多くした赤色の線に着目するとCTL実験を示す緑線よりも上側部分に見られる傾向にある。一方，雲粒数を少なくした青色の線に着目すると，緑線よりも下側部分に見られる傾向にある。該当しない事例や時間帯もあるが，雲粒数が多い場合は中心気圧が弱まり，少ない場合は中心気圧が強まる傾向が確認された。また，中心気圧の変化幅は最大で約3 hPaの増減であった。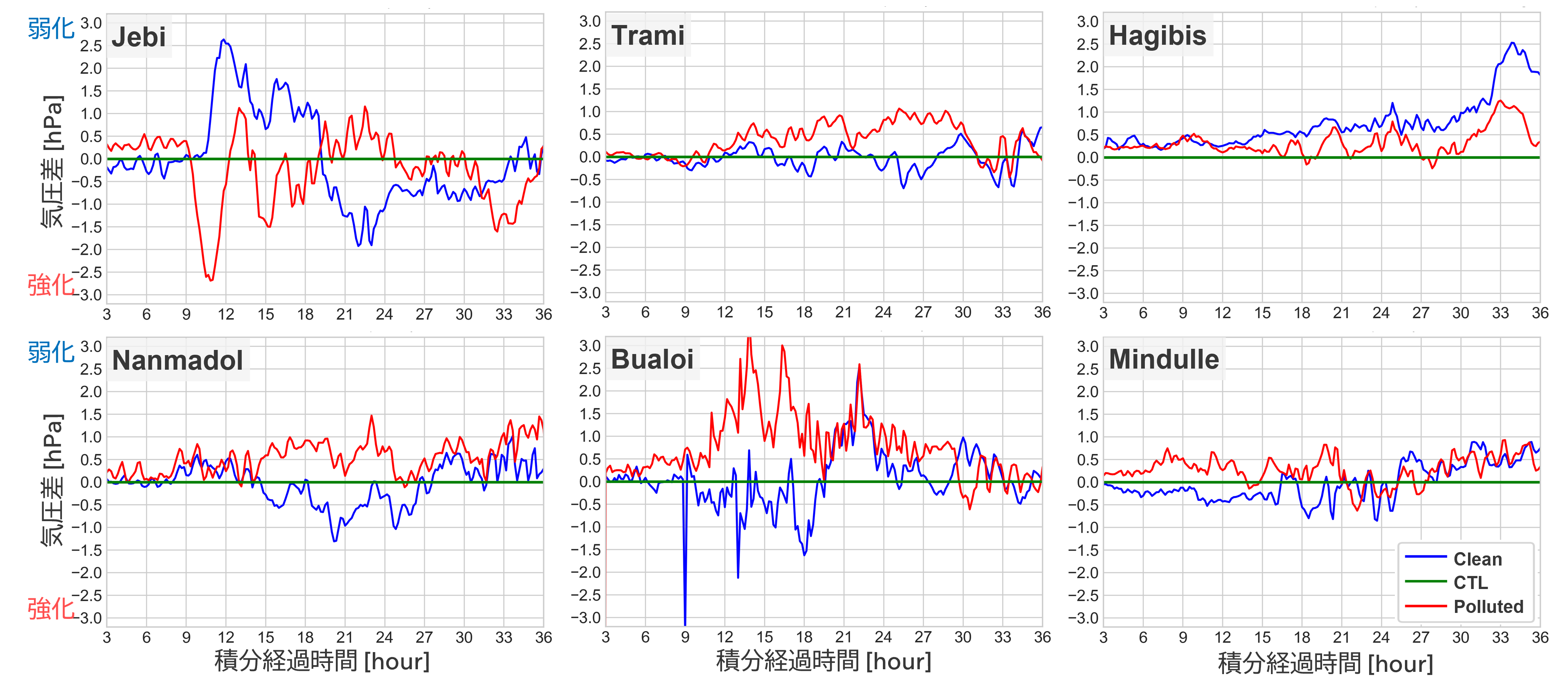

▲図5：CTL実験を基準とした台風中心の差分の時間変化。
　

雲粒数の増減による雲の鉛直分布の変化

　台風の中心気圧の変化が見られたとき，雲粒の数の違いによる台風の雲の鉛直構造はどのような変化をするのかを調べた（図6）。図6はBualoi事例の6時間平均した全凝結物混合比と鉛直風の半径高度断面図を示す。Bualoi事例は既往研究で示された中心気圧の応答が確認された事例であり，そのうち顕著に応答が確認された6時間（積分開始14時間後から20時間後）で平均している。全凝結物混合比（図6 a-c）について，壁雲域に対応する台風中心から0.5°から1.0°の間における全凝結物混合比の出現高度が，Cleanでは約11 km，CTLでは約12 km，Pollutedでは約15 kmであった。すなわち，壁雲での雲の高さがCTLと比較して，雲粒数が少ないと低下し，高いと上昇した。このような分布の違いが見られたとき，凝結物が運ばれるための対流に違いが見られる可能性が考えられることから，次に鉛直流（図6 d-f）の変化を確認した。台風中心から0.5°から1.0°の間における強い上昇流が到達する高度が，CTL実験では12.5kmまででしたが，Cleanではその高度にまで達しておらず，Pollutedではその高度を超えてより上層にまで達していた。つまり，壁雲での強い上昇流の位置が，雲粒数が少ないと低下し，高いと上昇した。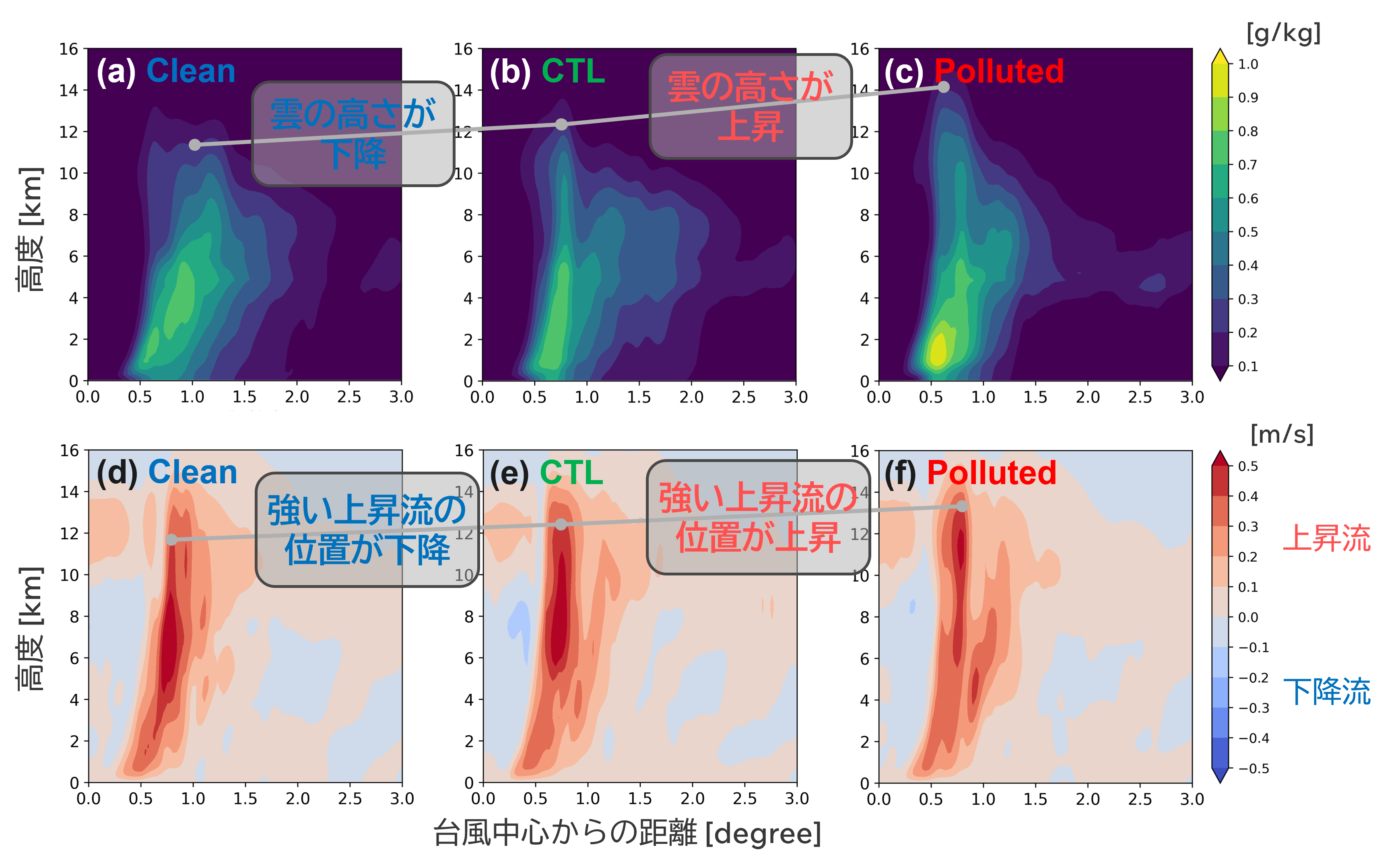

▲図6：方位角方向に6時間平均した全凝結物混合比（水物質量；a-c）と鉛直風（d-f）の半径高度断面図。
　

雲粒数の増減による台風の熱力学的構造の変化

　雲粒の数の違いおよび凝結物の分布の変化が台風の熱力学的構造にどのような影響をもたらしたかを調べるために，台風中心から距離300 kmの領域での平均温位からの偏差を確認した（図7）。台風中心付近の高度約5 km で極大が見られたCTLに対してCleanではより上層（図7d）で，Pollutedではより下層（図7e）で極大が表れ，雲粒数の違いにより台風暖気核の位置に変化が見られた。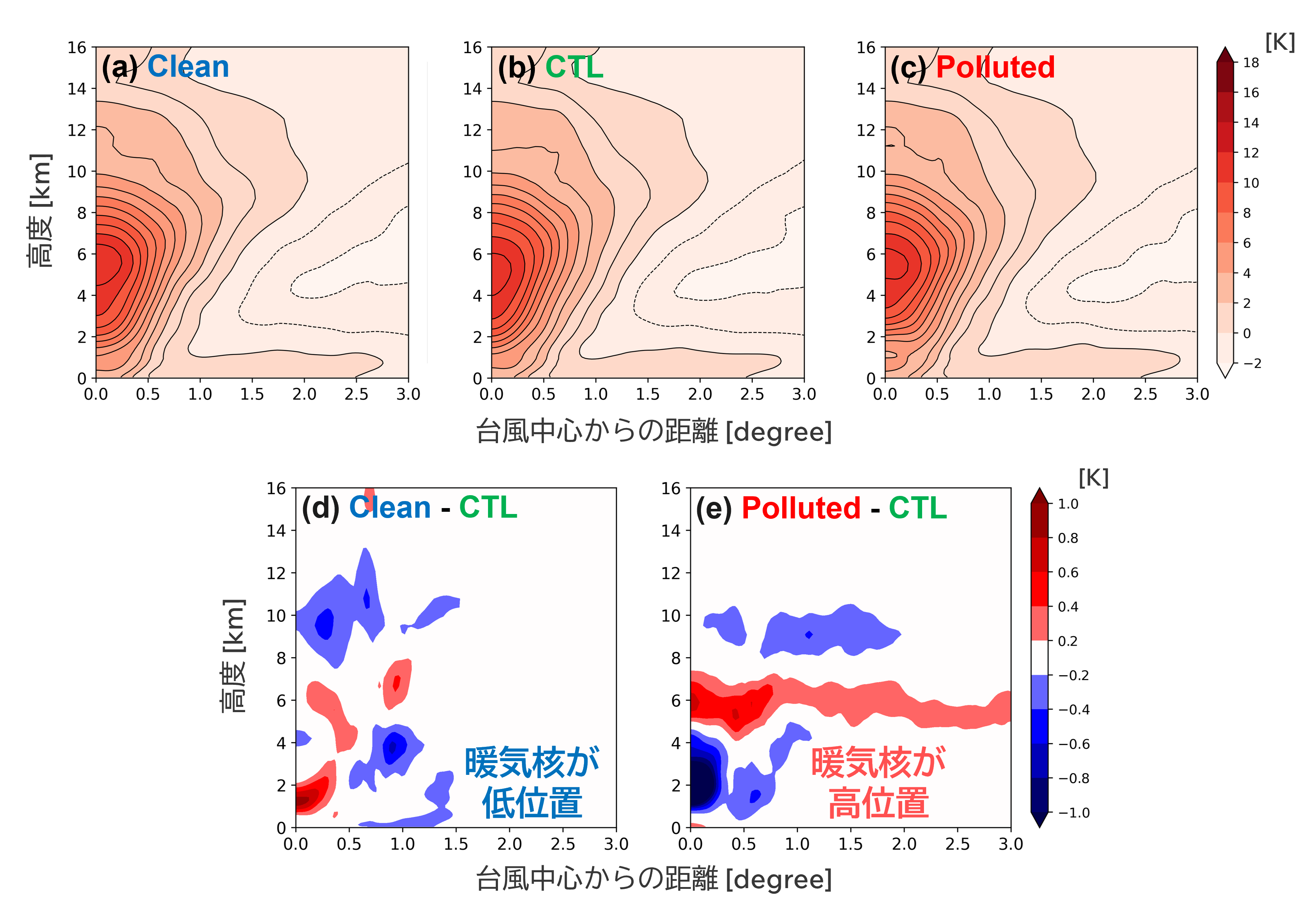

▲図7：方位角方向に6時間平均した温位偏差（a-c）の半径高度断面図と
CTLとの差（d:Cleanの差分, e:Pollutedの差分）。
　

Discussion

　シミュレーションされた台風にて，感度実験の間で確認された温度変化と気圧変化の関係を温度変化と気圧変化の関係式を用いて定量的に評価した。シミュレーションされた台風におけるCTLに対する温度変化とそれによる気圧変化の関係は，理論式で算出される関係と一致し，またCTLとの気圧の差分量は理論式で算出される差分量と概ね一致していた。
　本研究における雲粒数濃度の違いによる台風の中心気圧に変化が起きたメカニズムを考察する（図8）。雲粒や雨粒などの凝結物がより上層に運ばれ，台風の中心では相対的により上層で高温域が表れた。すなわち，台風中心における台風暖気核の高度に変化が起こった。このことから，雲粒の数の違いが台風の中心付近における雲の鉛直構造を変化させ，台風の熱力学的構造に影響を与えたことにより，中心気圧に違いが見られたと考えられる。

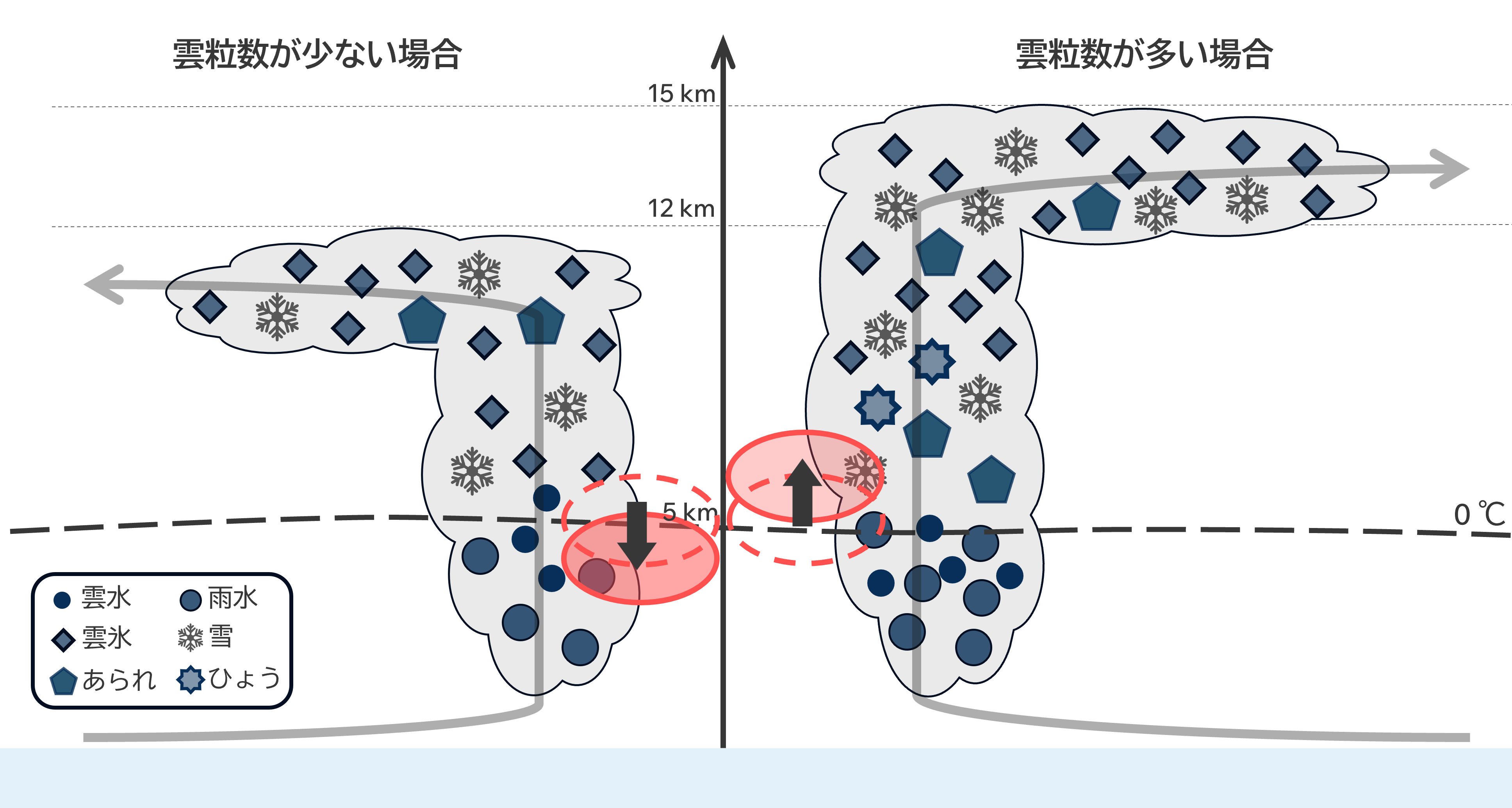
▲図8：雲粒数の違いによる雲の構造の変化と中心気圧への応答を示す模式図。
　

Summary

雲粒数の増減による中心気圧の変化を雲解像モデルを使用した数値実験により調べた。
雲粒数が多い場合に中心気圧が弱まり，少ない場合に中心気圧が強まる傾向が見られた。
雲粒数の増減により中心気圧に変化が見られた時間帯では，凝結物が到達する高度および強い対流の位置が，雲粒数が少ないときは低下し，多いときは上昇した。
雲粒数の違いが雲構造の変化をもたらし，台風の熱力学的構造に変化を生じさせたため，中心気圧に違いが起きたと考えられる。

Reference

Khain, A. P., K. D. Beheng, A. Heymsfield, A. Korolev, S. O. Krichak, Z. Levin, M. Pinsky, V. Phillips, T. Prabhakaran, A. Teller, S. C. van den Heever, J.-I. Yano, 2015: Representation of microphysical processes in cloud-resolving models: Spectral (bin) microphysics versus bulk parameterization, Rev. Geophys., 53, 247–322.
村上正隆，吉住蓉子，長谷川晃一，紀平旭範，榊原篤志，橋本明弘，篠田太郎，加藤雅也，2021：ダブルモーメント雲微物理パラメタリゼーション（CReSS-4ICE）の開発．日本気象学会大会講演予稿集，119，169．
Rosenfeld, D., U. Lohmann, G. B. Raga, C. D. O’Dowd, M. Kulmala, S. Fuzzi, A. Reissell, M. O. Andreae, 2008: Flood or drought: How do aerosols affect precipitation? Science, 321, 1309–1313.
Tsuboki, K., 2008: High-resolution simulations of high-impact weather systems using the cloud-resolving model on the Earth Simulator (Hamilton, K., Ohfuchi, W., ed.). High Resolution Numerical Modeling of the Atmosphere and Ocean, Springer, 141–156.
Twomey, S., Squires, P.,1959: The Influence of Cloud Nucleus Population on the Microstructure and Stability of Convective Clouds. Tellus, 11, 408-411.
Twomey, S., 1977: The Influence of Pollution on the Shortwave Albedo of Clouds. J. Atmos. Sci., 34, 1149–1152.