アンサンブル予測を用いた台風発生・進路予測の
不確実性評価
横浜国立大学大学院 環境情報学府
川端康弘
第1章 序論
台風は暴風や大雨、高潮など大きな災害をもたらすことがある。台風による災害リスクを低減するためには、台風予測の理解と高度化を図ることが重要である。台風の予測には不確実性を伴い、予測に関する知見や情報の利活用の拡充が求められる。これまで台風の予測の不確実性を見積もるために、アンサンブル予測の有効性が議論されてきた。しかし、台風の発生・進路予測の不確実性に関する統計的な検証は十分に行われておらず、定量的な評価や気象場の理解が不足している。
そこで本研究では、まずアンサンブル予測に基づく発生予測にどの程度の不確実性が存在するかを調査する。予測における台風発生の有無や位置に関するばらつきは、その後の進路予測に影響すると考えられる。進路予測については、アンサンブル予測のメンバーの空間分布を解析し、予測のばらつきの特徴を見出す。そして、進路予測の不確実性の表現方法を提案する。また、台風の発生・進路予測の背景要因といった予測に向けた知見を蓄積するために、過去の台風活動の長期的傾向や地域的偏りについて統計的特徴を整理する。以上の解析を通して、台風の発生・進路予測における不確実性の構造を明らかにし、大気の環境場との関係を示す。これにより、アンサンブル予測に基づく台風発生・進路予測の不確実性の理解と、進路予測の情報改善に資する知見を提供することを目的とする。
第2章 データと解析手法
2.1 データ
2.1.1 アンサンブル予測データ
台風の発生予測および進路予測の不確実性の解析に用いたデータは、海外の数値予報センターも含めた複数のアンサンブル予測の台風トラックデータである。気象庁(JMA)、欧州中期予報センター(ECMWF)、米国環境予測センター(NCEP)、英国気象局(UKMO)のデータである。マルチセンターアンサンブルはこれら4つのアンサンブル予測を組み合わせた手法である。
2.1.2 台風ベストトラックデータ
アンサンブル予測の検証に用いたデータは、事後解析による確定値(ベストトラック)である。これは台風について、速報解析時点およびそれ以降に入手したデータを用いて事後検討し、詳細に解析したものである。
2.1.3 ドボラック再解析データ
台風活動の統計解析に用いたデータは、気象庁が長期にわたり一貫した方法で作成したドボラック再解析データである。これは、複数の予報官が衛星画像を用いて、1987年から2016年までの台風の強度推定をドボラック法と呼ばれる手法により改めて作成し直したものである(Nishimura et al. 2023)。
2.2 解析手法
2.2.1 台風の発生予測確率の算出と検証手法
台風の発生予測検証の解析期間は2017~2020年の4年間である。台風発生の予測確率は次のようにして決定する。まず、ベストトラックにおいて、熱帯低気圧が最初に解析された時刻の位置を中心として、半径500kmの範囲を探索する。次に、各予測時刻(Forecast Time:FT)において、各数値予報センターのアンサンブルメンバーのうち、この円内に入っているメンバーの数を算出することで予測確率を計算する。
また、発生予測の検証に頻度バイアスとカテゴリー検証を行う。台風の発生を過大もしくは過小に予測しているのか評価するために、頻度バイアスを算出する。頻度バイアスは、実際に台風が発生した領域(格子点の数)に対する、アンサンブル予測が台風を予測した領域(格子点の数)の比で定義される(Yamaguchi et al. 2015)。台風の発生を予測した格子点の数は、予測された確率値で重み付けされる。頻度バイアスが1より大きい場合は、アンサンブル予測が実際に発生した台風よりも多く予測する傾向があることを意味する。カテゴリー検証においては、2×2分割表を用いてスレットスコアを算出する。スレットスコアは予測または実況で「現象あり」の場合の予測適中事例数に着目して予測精度を評価する指標であり、最大値の1に近いほど、予測精度が高いことを示す。
2.2.2 台風の発生環境場の検出
熱帯低気圧の発生には大気環境場との関連が報告されている。Ritchie and Holland(1999)は環境場として対流圏下層の流れパターンを5つのカテゴリーに分類した。すなわち、シアーライン(SL)、東西風合流域(CR)、モンスーンジャイア(GY)、偏東風波動(EW)、先行する台風からのロスビー波エネルギーの分散(PTC)である。Yoshida and Ishikawa(2013)は、Ritchie and Holland(1999)の5つのパターンを客観的に分類し、それぞれの環境場における熱帯低気圧の統計的特徴を明らかにした。本研究においても、台風発生時の環境場について5つの下層流れパターン(SL、CR、EW、GY、PTC)に分類し、発生予測との関係を調査する。
2.2.3 台風の進路予測誤差の算出および予報楕円の作成
台風の進路予測検証の解析期間は2016~2018年の3年間である。マルチセンターアンサンブルを用いて予報円と予報楕円の面積を比較する。予報円はアンサンブル平均の位置を中心に、アンサンブルメンバーの70%が含まれる円として定義する。予報楕円についても同様である。予報楕円を決定するパラメータは、長軸、短軸、回転角の3つである。各予測時刻において、これらのパラメータを変化させ、アンサンブルメンバーの70%が含まれる領域の面積が最も小さくなるように予報楕円を作成する。
また、アンサンブルメンバーのばらつき具合を示す指標としてアンサンブルスプレッドを算出する。アンサンブルスプレッドは、個々のアンサンブルメンバーの位置とアンサンブル平均位置との距離の標準偏差である。予報楕円を調査するにあたり、アンサンブルスプレッドを台風の進行方向成分(Along Track:AT)と進行方向に直交する成分(Cross Track:CT)に分解する。アンサンブル平均の予測誤差についても、AT方向とCT方向に分解する。
第3章 台風発生予測の精度検証
3.1 台風の発生予測確率
アンサンブル予測を用いて台風の発生予測の特徴を調査した。図1は各数値予報センターにおける台風発生の平均予測確率を示す。各予測時間における確率は、全ての台風について平均したものである。0時間先予測(FT0)は、ベストトラックで初めて熱帯低気圧が解析された時刻(すなわち台風の発生)である。例えば、72時間先予測(FT72)は台風発生の3日前からの3日先予測を示す。JMA、ECMWF、NCEPの予測確率は予測時間とともに減少しているが、UKMOの予測確率は4日先予測(FT96)までほぼ一定である。5日先予測(FT120)における平均予測確率は全てのセンターで20%未満であり、1週間先予測(FT168)ではNCEPを除いて10%未満である。
図2は1週間先(FT168)の予測について個々の台風の予測確率を示す。75パーセンタイル値は10%を下回っているが、いくつかの台風については予測確率が高くなっていた。このことは、1週間先の予測であっても、事例によっては台風の発生を予測できる可能性があることを意味している。
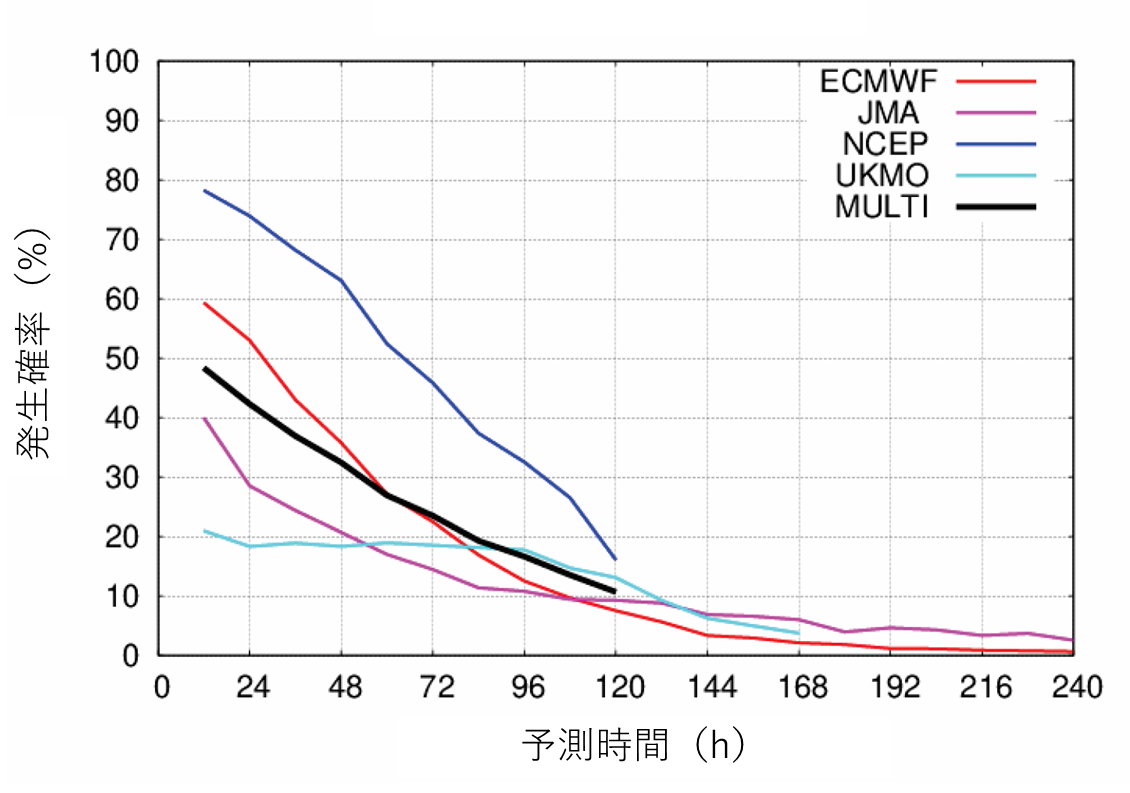
図1. 台風の平均発生予測確率。
MULTIはマルチセンターアンサンブルを示す。
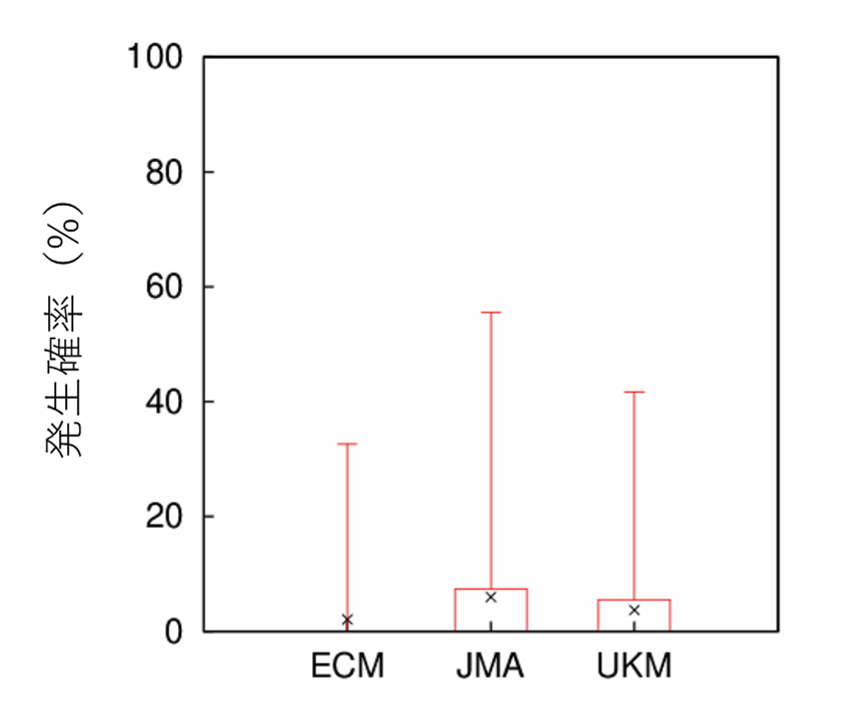
図2. 各台風の168時間予測における発生予測確率の箱ひげ図。
×印は予測確率の平均である。ECMはECMWF、UKMはUKMOを示す。
3.2 発生予測検証
台風の発生予測確率は平均的にはNCEPが高い傾向にあった。NCEPが台風を過大もしくは過小に予測しているのか評価するために頻度バイアスを調査した。図3は各予報センターにおける予測確率の頻度バイアスを示している。NCEPの頻度バイアスは1よりも大きく、他の予報センターよりも大きい傾向にある。この結果は、NCEPが台風の発生を過大に予測していることを示唆している。
次に、台風の発生予測において、各数値予報センターでどの程度予測スキルがあるか調べた。図4は各センターとマルチセンターアンサンブルにおけるスレットスコアを示している。ベストトラックにおいて台風の発生位置を中心に半径500km以内に50%以上の確率で予測できた場合、適中と定義した。全ての予報センターとマルチセンターアンサンブルのスレットスコアは、予測時間が長くなるにつれて減少する。マルチセンターアンサンブルのスレットスコアを各センターと比較すると、3日先予測(FT72)まで最も高い値となっており、予測スキルが高いことを示している。
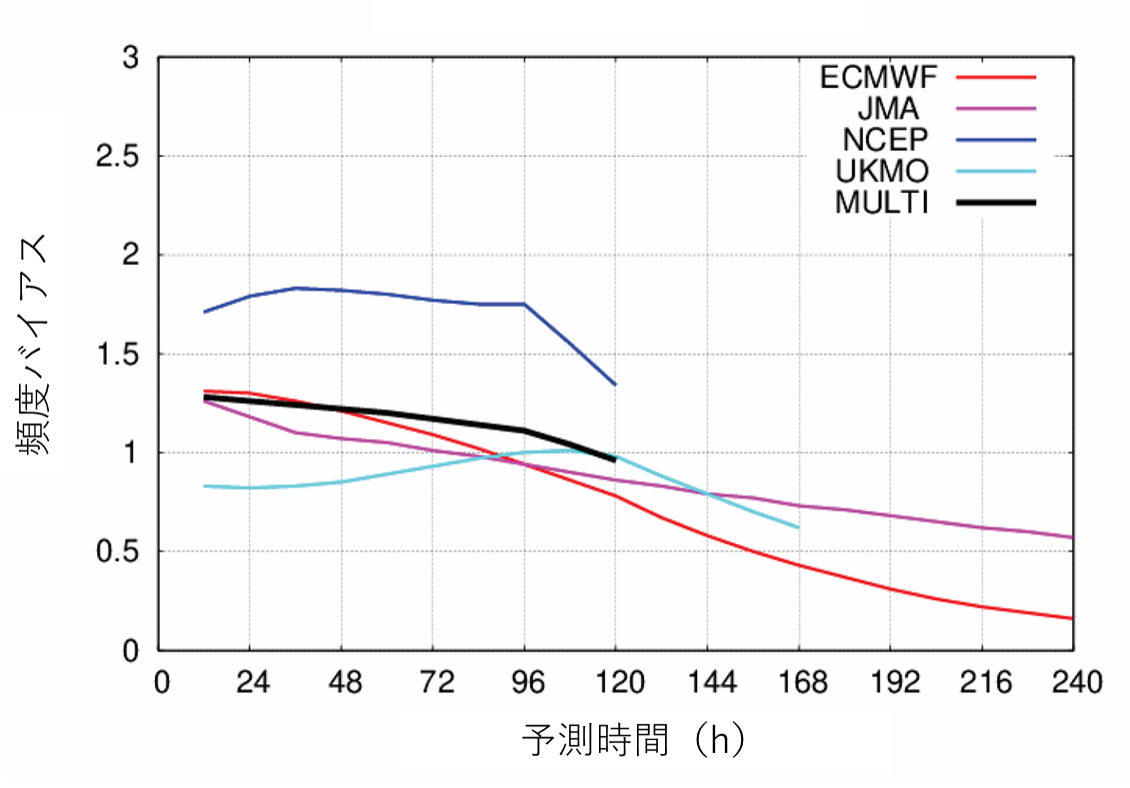
図3. 台風発生予測における頻度バイアス。
MULTIはマルチセンターアンサンブルを示す。
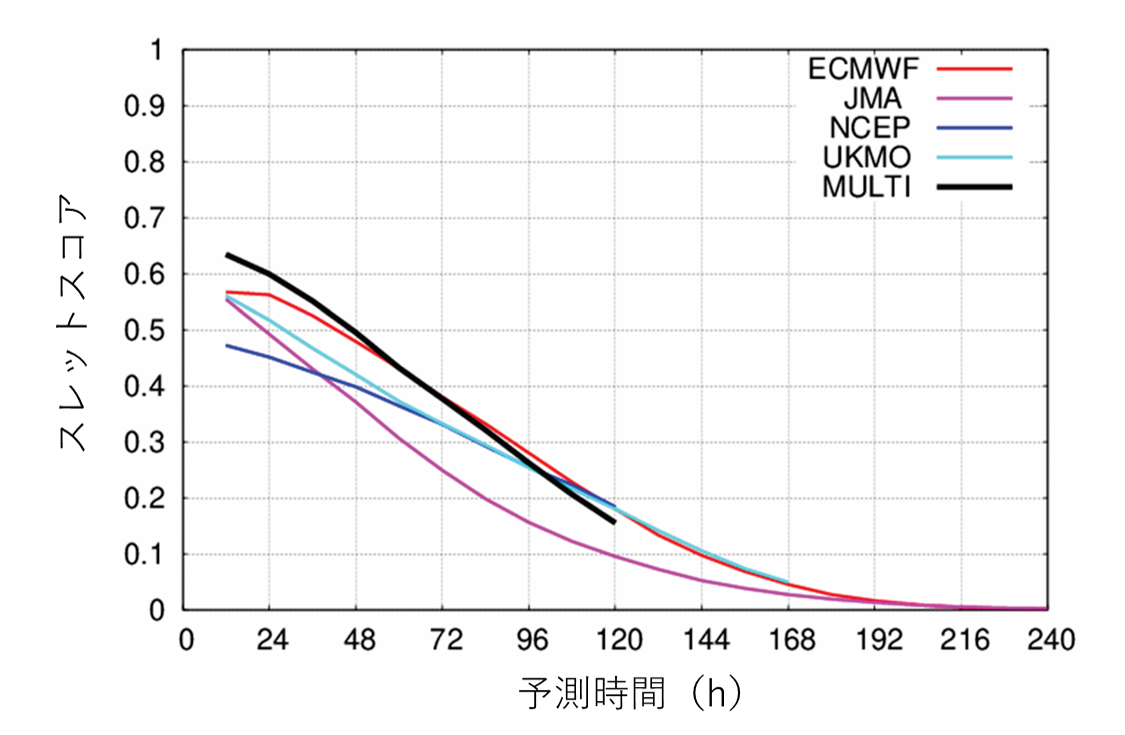
図4. 台風発生予測検証におけるスレットスコア。
MULTIはマルチセンターアンサンブルを示す。
3.3 台風の発生環境場との関係
各数値予報センターの予測から得られる台風発生の特徴について、大気環境場との関連を把握するために、台風の発生予測確率と主要な下層流れパターンの依存性を調査した。図5は各数値予報センターにおける各流れパターンごとの台風の3日先予測の平均予測確率を示している。シアーラインパターン(SL)で発生した台風が最も多く、先行台風パターン(PTC)の台風が最も少ない。全てのセンターにおいて東西風合流域パターン(CR)で発生した台風の予測確率が最も高い。
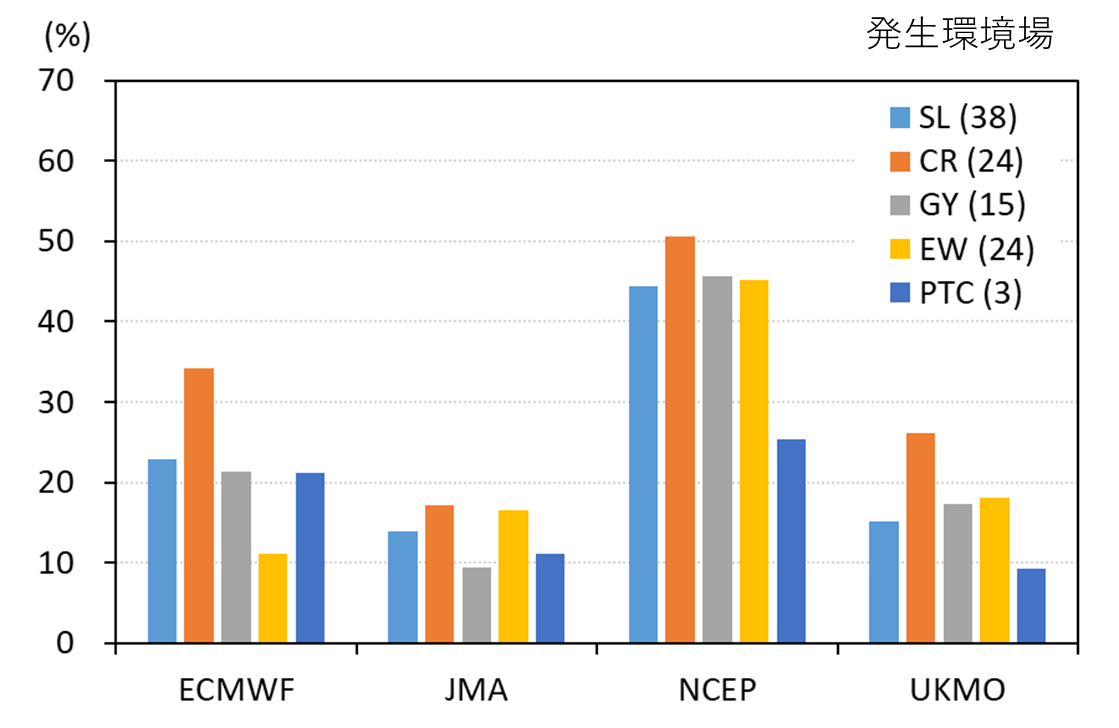
図5. 台風発生環境場の主要な流れパターンと3日先予測の平均確率。
括弧は台風の事例数を示す。
3.4 台風の強さの階級がTropical Stormの場合の検証
台風発生の定義は、台風がベストトラックで初めて熱帯低気圧として記録された時刻とした。一方、台風の階級が「Tropical Storm」の強さに発達するタイミングも防災上重要であり、この時刻では台風に名前が付けられる。そこで、「Tropical Storm」に発達する時刻を基準として、台風の発生予測確率を調べた。図6は台風発生の平均予測確率を示す。1日先予測(FT24)における平均予測確率は数値予報センターによって異なるが、全てのセンターで60%を超えている。5日先予測(FT120)における平均予測確率は15~35%の範囲であり、1週間先予測(FT168)では10%未満となっている。

図6. 台風の階級「Tropical Storm」の強度における平均発生予測確率。
第4章 台風進路予測の不確実性評価
4.1 アンサンブル平均の予測誤差
4つの数値予報センター(JMA、ECMWF、NCEP、UKMO)のアンサンブル予測、すなわちマルチセンターアンサンブルを用いて、台風進路予測の不確実性を調査した。図7は5日(120時間)先までのアンサンブル平均予測の位置誤差を示す。誤差はAT方向とCT方向に分解している。どの予測時間においてもAT方向の平均誤差はCT方向の平均誤差よりも大きい。台風の進路予報円は誤差が等方性であるという仮定が含まれているが、この結果は誤差が等方的でなく、CT方向よりもAT方向の誤差の方が大きくなることを示唆している。
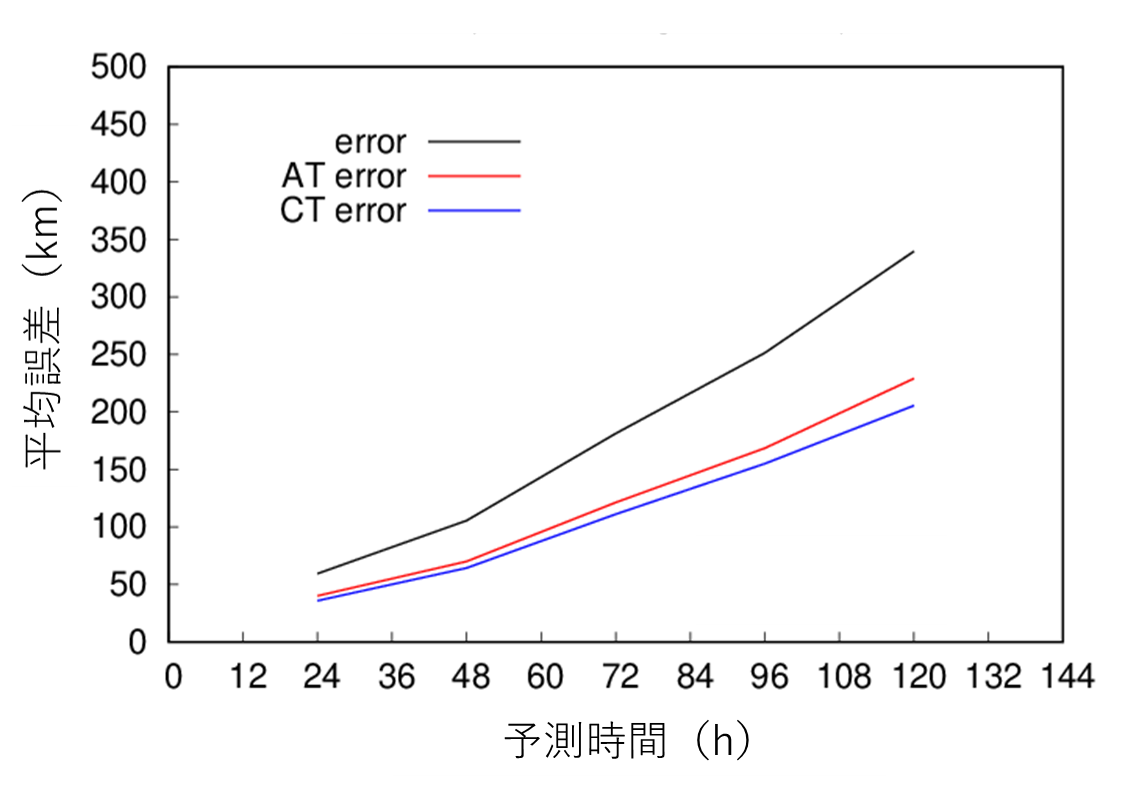
図7. アンサンブル平均予測における台風進路の平均誤差。
4.2 台風の進行方向と直交方向の不確実性
アンサンブル予測の不確実性を表現するために台風の進路の予測領域を楕円形で示し、予報円と比較した。図8はマルチセンターアンサンブルにおける台風進路の72時間予測の予報円と予報楕円の例を示す。2016年台風第16号(T1616)について、アンサンブルメンバーのばらつきは、進行方向成分(AT方向)の方が進行方向に直交する成分(CT方向)よりも大きい。これは台風がいつ来るか、すなわち移動速度に関する不確実性が、台風がどちらに向かうか、すなわち移動方向に関する不確実性よりも大きいことを示している。一方、2018年台風第13号(T1813)について、アンサンブルメンバーのばらつきは、CT方向の方がAT方向よりも大きい。この例では、台風がいつ来るかという不確実性よりも、台風がどちらに向かうかという不確実性の方が大きい。
図9は台風進路予測の72時間予測におけるアンサンブル平均した位置を示す。AT方向の不確実性を持つ事例の方が、CT方向の不確実性を持つ事例よりも多い。スプレッド比AT/CTの値が大きい領域は特に中緯度帯となっている。AT方向で大きな不確実性を持つことは、アンサンブル平均の進路予測誤差がAT方向で大きく、特に中緯度帯で顕著であることと整合的である。
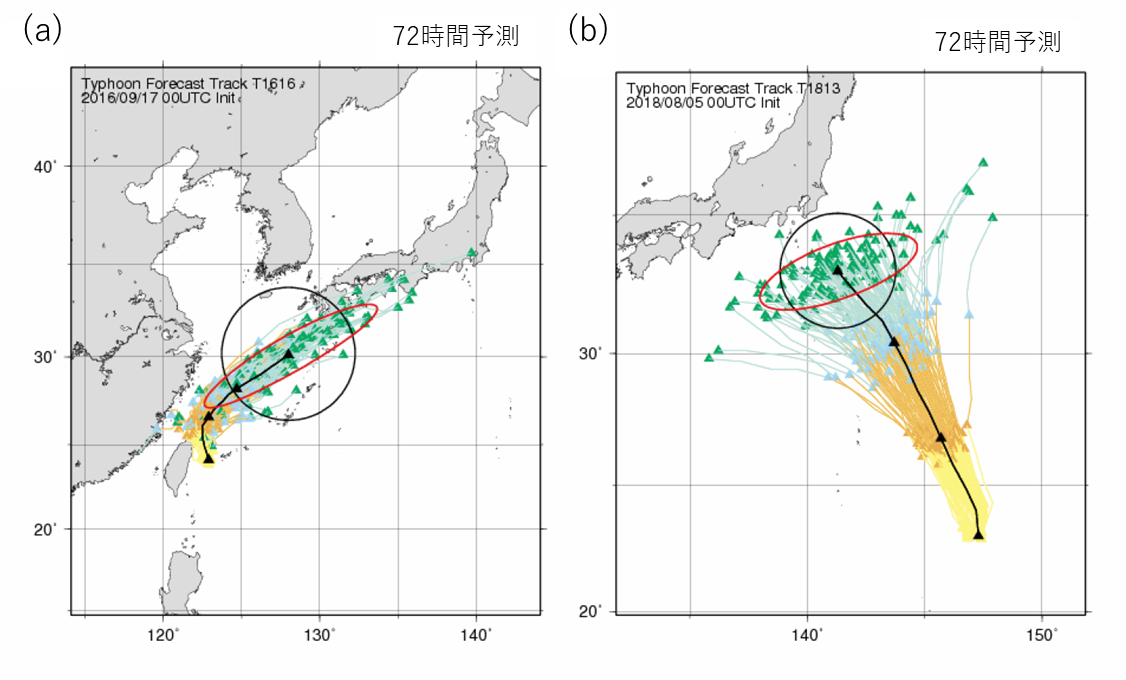
図8. 台風進路の72時間予測における予報円と予報楕円の例。
(a)T1616。(b)T1813。黒色の三角形はアンサンブル平均を表す。
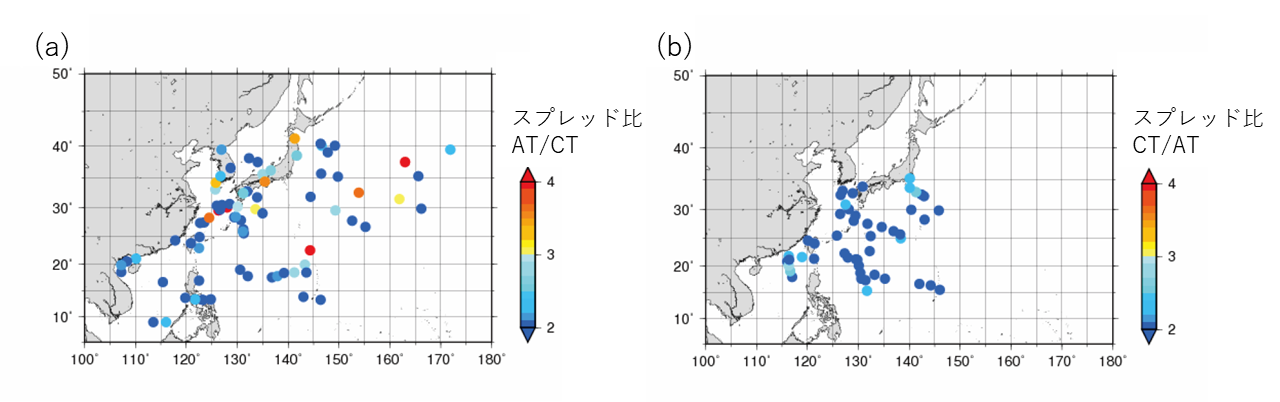
図9. 台風進路の72時間予測におけるアンサンブル平均の位置。
(a)CT方向に対するAT方向のアンサンブルスプレッド比(AT/CT)が1.5以上の予測事例。
(b)AT方向に対するCT方向のアンサンブルスプレッド比(CT/AT)が1.5以上の予測事例。
4.3 アンサンブルスプレッドと誤差の関係
アンサンブルスプレッドはアンサンブルメンバーの広がりの指標である。図10はAT方向およびCT方向におけるアンサンブルスプレッドとアンサンブル平均の位置誤差の関係を示す。アンサンブル予測のスキルが良い場合、プロットは対角線に近くなる。AT方向およびCT方向の両方において、平均的なスプレッドは、大きなスプレッド区分において平均誤差よりも大きい。これはアンサンブル予測が過分散的であることを示唆している。しかし、相関係数は正の値となっており、マルチセンターアンサンブルが、台風の進路予測において大気の流れに応じた不確実性を予測できることを示している。
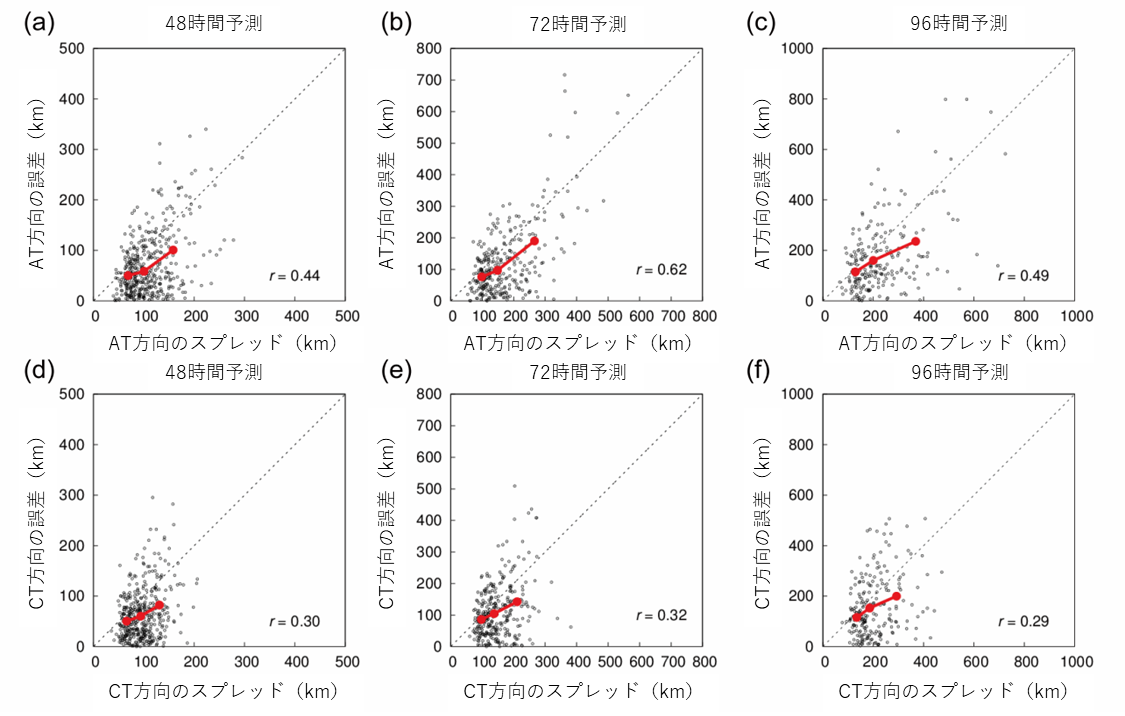
図10. AT方向およびCT方向における予測時間別のアンサンブルスプレッドとアンサンブル平均の予測誤差の関係。
赤線はスプレッドを3つのカテゴリーに分割し、各区分におけるスプレッドと誤差の平均を示す。
各パネルの r は相関係数を表す。
4.4 予報楕円の有効性
予報円の代わりに予報楕円を採用することで、どの程度面積が減少しているか評価するために面積を比較した。予報円と予報楕円は、いずれもアンサンブルメンバーの70%が含まれるように作成したが、的中率は70%ではなかった。ここで、的中率はベストトラックに基づく台風の中心位置が、予報円もしくは予報楕円の内側に入る割合として定義した。予報円と予報楕円の面積を同じ基準で比較するために、それぞれの半径に定数を掛けて、的中率が70%になるように大きさを調整した。このようにして改めて面積を比較したところ、予報円の代わりに予報楕円を採用することで、面積は3日先予測で16%、4日先予測で15%、5日先予測で24%減少した。
第5章 台風活動の統計解析
5.1 強い台風の長期変化
ドボラック再解析データを用いて、ハリケーンスケール・カテゴリー4以上の強い台風の長期変化傾向を調べた。これは、生涯最大CI数が6.0以上の台風に相当する。ここで、CI数(Current Intensity number)は台風の強度の指標である。図11は強い台風の数と、各年における全ての台風に占める強い台風の割合の経年変化を示す。強い台風の長期変化では、数および割合のいずれにおいても、顕著な増減傾向は見られない。
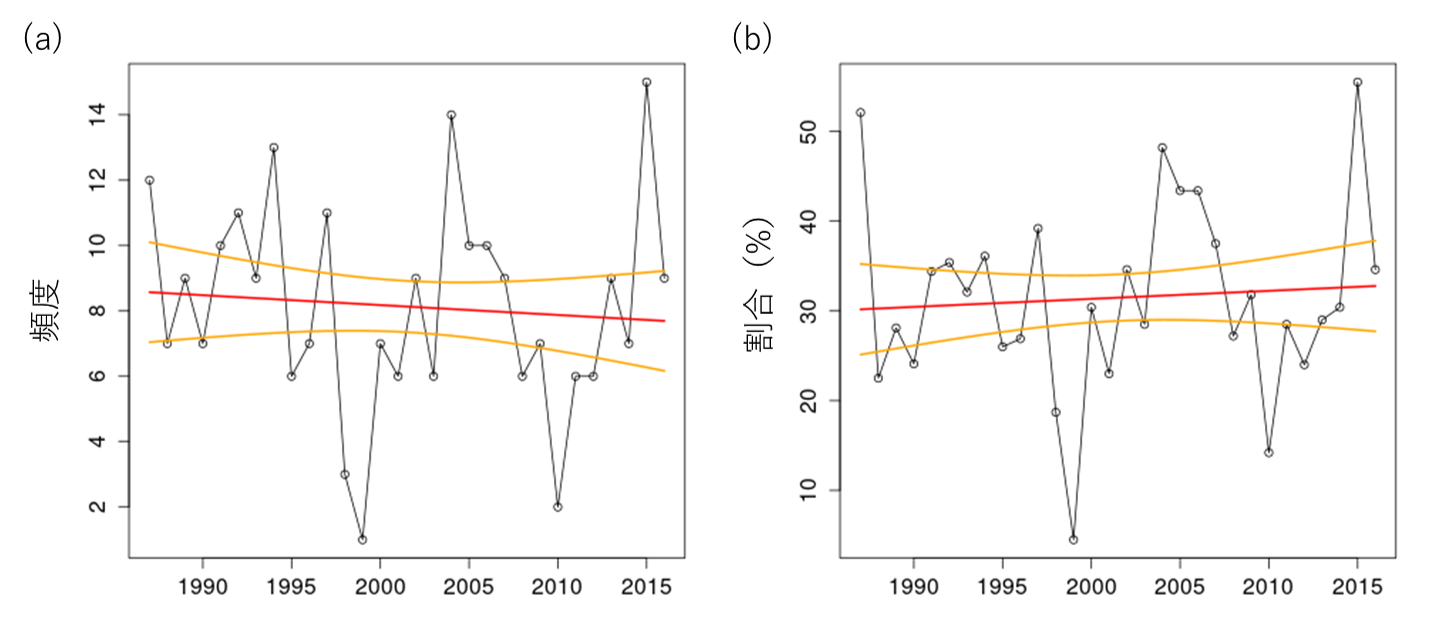
図11. カテゴリー4以上(生涯最大CI数が6.0以上)の強い台風の経年変化。
(a)強い台風の数。(b)各年の全ての台風に対する強い台風の割合。
赤線は線形回帰直線、橙線は回帰直線の90%信頼区間を示す。
5.2 空間分布の変動
強い台風の空間分布の時間変動を調査した。図12は強い台風の年平均発生位置の時系列を示している。発生は、ドボラック再解析データにおいて各台風のCI数が初めて2.0以上になった時の位置と定義した。発生の緯度と経度の線形回帰直線の信頼区間の結果から、強い台風の発生場所は西に移動する傾向が見られた。
また、図13は強い台風が最初に生涯最大強度に達した年平均位置の経年変化を示している。強い台風が最大強度に達する位置は北西方向に移動する傾向が見られた。
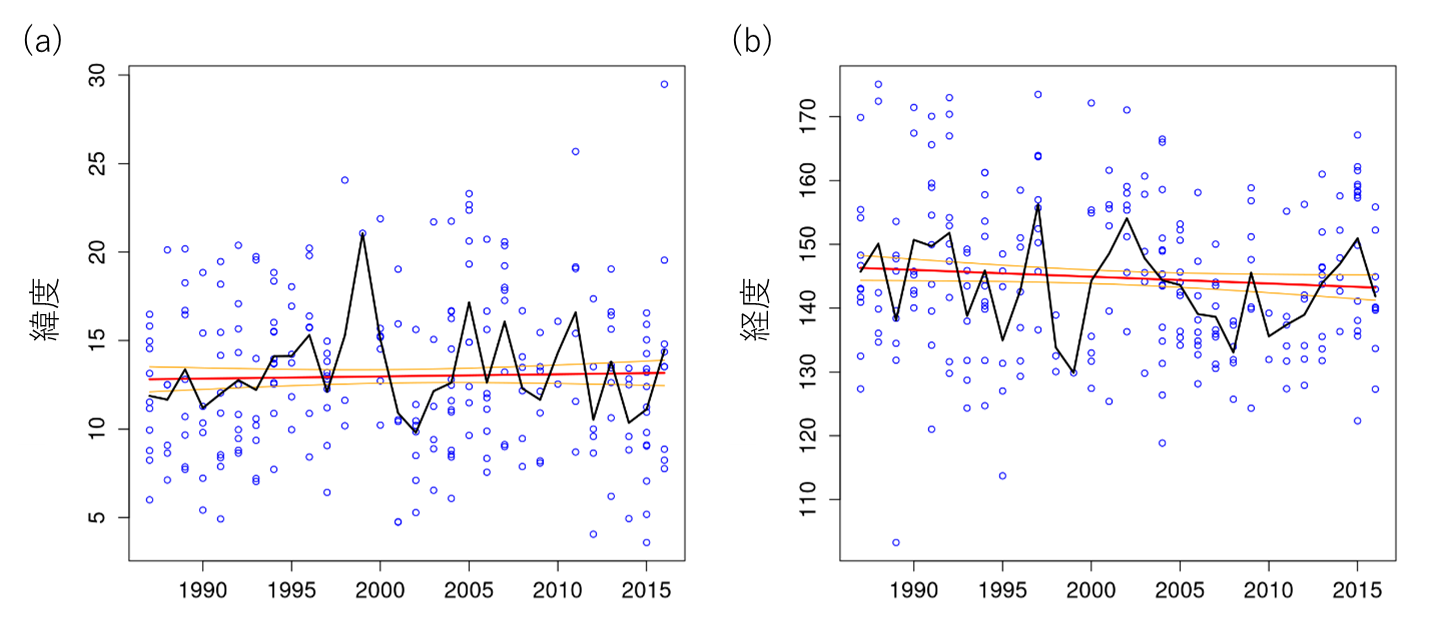
図12. 強い台風における平均発生位置の経年変化。
(a)緯度(°N)。(b)経度(°E)。丸印は各年の全データ、黒線は平均値を表す。
赤線は線形回帰直線、橙線は回帰直線の90%信頼区間を示す。
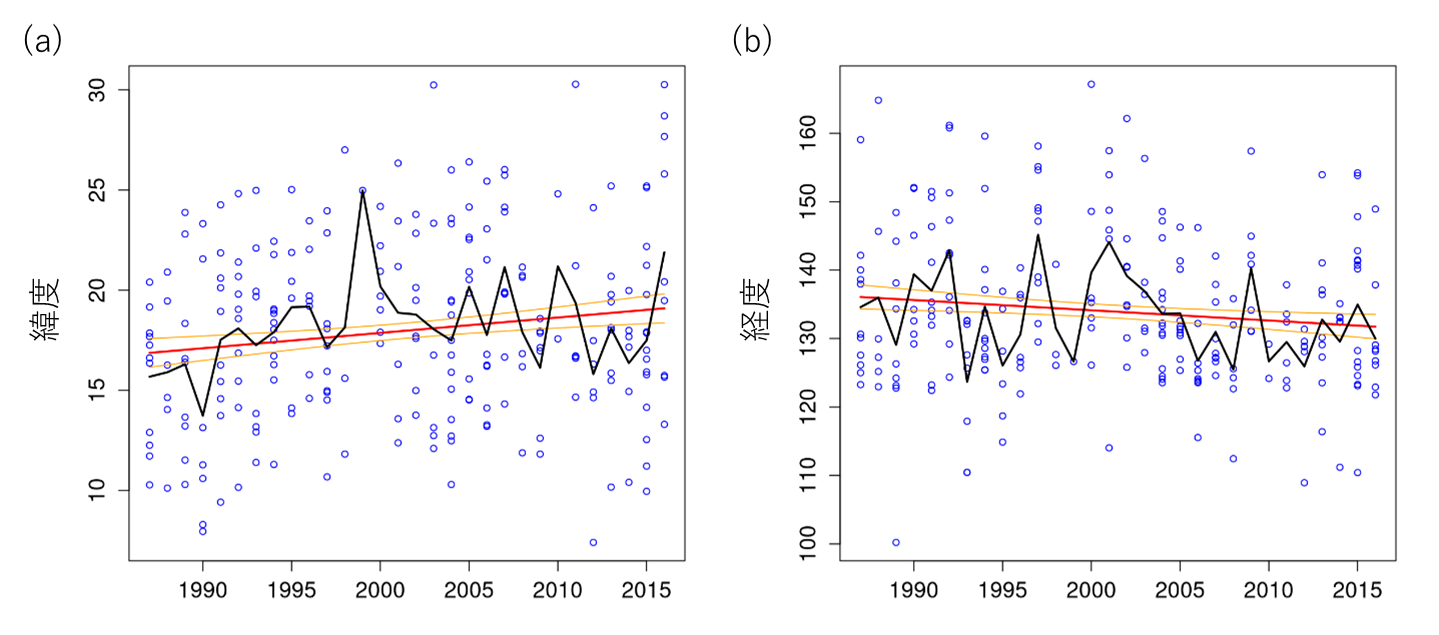
図13. 強い台風における最大強度に達した時の平均位置の経年変化。
(a)緯度(°N)。(b)経度(°E)。丸印は各年の全データ、黒線は平均値を表す。
赤線は線形回帰直線、橙線は回帰直線の90%信頼区間を示す。
5.3 発生位置の変化
強い台風の発生位置と生涯最大強度の位置に関する30年間の変化の結果から、北西太平洋における強い台風の分布が変化した可能性が示唆される。そこで、強い台風の割合が局所的にどのように変化したかを調査した。図14は解析期間前半と後半における台風の発生位置を、生涯最大強度で色付けして示している。全ての領域で発生した台風全体に占める領域IVとV(越境台風)の強い台風の割合は、解析期間の前半よりも後半の方が低くなっていた。一方、領域IIとIIIで発生した強い台風の割合は、解析期間の前半よりも後半の方が高くなっていた。
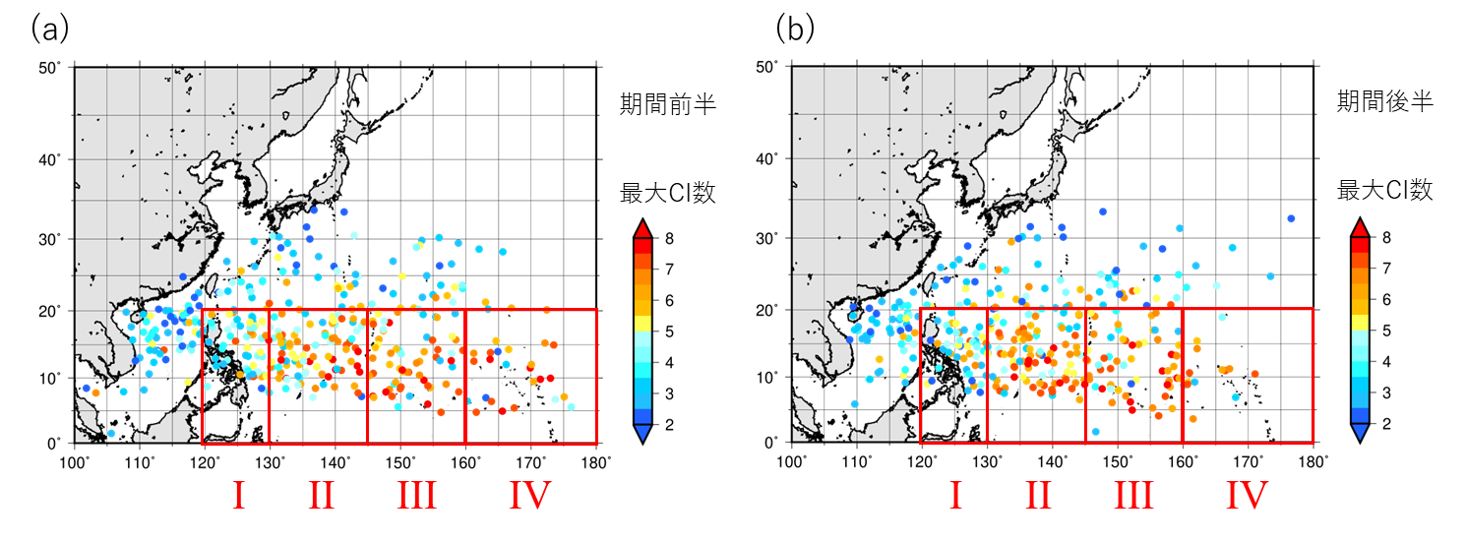
図14. 台風の発生位置の分布。
(a)1987~2001年。(b)2002~2016年。
第6章 議論
6.1 台風の発生予測と発生環境場に関する考察
台風発生の平均予測確率が最も高かった環境場は東西風合流域パターンであった。東西風合流域パターンに関連する環境場は、貿易風による東風とモンスーントラフに由来する西風が合流する大きな領域によって特徴づけられる。この風の場が長期間継続するため、台風の発生に適した環境が持続する。したがって、台風の発生は数日前から予測でき、より長いリードタイムを確保できると考えられる。Yoshida and Fudeyasu(2020)は、台風の発生スコアの格子点版を開発し、環境場の時空間変動を調査した。台風の発生スコアは、各格子点、各時刻で計算される。これらのスコアは、環境場の空間分布を表すことができ、任意の地点における台風発生の可能性を推定することができる。東西風合流域パターンは他の環境場パターンよりもより大きな領域に支配され、その発生スコアは数日間高い状態が続くことが示されている。これらの特徴は、東西風合流域パターンにおける台風の発生予測確率が、他の環境場パターンよりも高いという結果と整合的である。
6.2 台風の進路予測における不確実性の構造
台風進路予測において、スプレッド比AT/CTの値が大きい領域は特に中緯度帯となっていた。中緯度では偏西風によるジェット気流が台風の進路に重要な役割を果たしていると考えられる。多くの台風は中緯度帯に移動し、総観場の影響を受ける(Ito et al. 2020)。中緯度でスプレッド比AT/CTが大きいことは、台風の動きが偏西風のジェット気流に強く影響され、ジェット気流の流れの方向に誤差が大きくなることを示唆している。一方で、CT方向の不確実性が大きい事例は、台風の転向点付近や指向流が弱い環境場が影響していると考えられる。
スプレッド比AT/CTが大きい場合は台風の進行方向に伸びた楕円で表現され、スプレッド比CT/ATが大きい場合は進行方向に直交する方向に伸びた楕円で表現される。予報楕円によって予測領域が縮小し、大気の流れに応じた予測の不確実性が表現できる。台風の移動速度と移動方向のどちらに不確実性が大きいかなど、不確実性に関する適切な情報を提供できれば、意思決定者や防災担当者にとって有益となる。予報楕円は防災上留意すべき領域を、より的確に示すことができ、台風進路予測の個性を持たせることが可能となる。
6.3 台風活動の気候学的特徴
過去の台風活動を把握することは、台風の発生・進路予測を気候学的な背景で評価する基礎資料となりうる。強い台風の発生位置は解析期間後半で局所的に西側にシフトしていた。1987~2016年の解析期間の後半では北西太平洋東部で台風の発生割合が低く、この要因として太平洋十年規模振動といった気候の自然変動による可能性がある。環境場の変化によって、北西太平洋の国々において台風接近までのリードタイムが短くなる状況下では、台風の発生予測に関する知見が重要となる。
第7章 結論
台風の発生・進路予測は重要な情報であり、十分なリードタイムや予測の信頼性があれば、台風による影響に備えることが可能になる。本研究では台風防災に資するため、アンサンブル予測を用いた台風発生・進路予測の不確実性を評価した。
まず、台風の発生予測の精度検証を行った。複数の数値予報センターのアンサンブル予測が事前にどの程度台風の発生を予測できたかを調査した。その結果、各センターで予測確率の差が大きく、不確実性の特徴が異なっていることがわかった。このことは、数値予測による台風の表現が各センターのアンサンブル予測によって大きく異なることを示している。
次に、台風の進路予測の不確実性評価を行った。台風の予測領域を楕円形にした場合の有効性について調査した。アンサンブル予測を用いることで、台風ごと、初期値ごとに異なる予測の不確実性を表現でき、大気の流れに応じて予報楕円を決定できることが示された。アンサンブルメンバーの分布をより適切に捕捉でき、台風の移動方向もしくは移動速度のどちらに不確実性が大きいかという予測の把握に有効であることが示唆された。また、予報楕円を用いることで、予報円と比較して、3~5日先予測で20%程度予測領域の面積が減少することが明らかとなった。
そして、予測に向けた知見を蓄積するために、台風活動の統計解析を行った。解析では台風の強度推定が時間的に均質なドボラック再解析データを用いた。ハリケーンスケール・カテゴリー4以上の強い台風に着目し、強い台風の長期変化傾向を調査したところ、台風の発生位置は局所的に見てより西側に移動し、最大強度に達した時の位置はより北西側に移動していることが明らかとなった。
台風の発生・進路予測の不確実性は、大気や海洋の環境場の影響を受けていることが示唆された。台風の発生予測では、東西風合流域パターンの環境場で平均的な発生予測確率が高いことがわかった。また、台風の進路予測において、台風の進行方向に沿った成分のアンサンブルスプレッドは中緯度帯で大きくなることが明らかとなった。この領域は偏西風の影響を受けやすく、ジェット気流が台風の進路に重要な役割を果たすことを示している。さらに、長期的な台風活動については、気候の自然変動が強い台風の発生位置と関係している可能性がある。
以上述べたように、台風の予測を高度化し、台風による被害を軽減するため、アンサンブル予測を用いて台風の発生・進路予測を新しい視点で評価するとともに、不確実性の表現方法を提案した。本研究では予測の不確実性に関する特徴を定量的に明らかにし、アンサンブル予測に関する新たな知見を提供した。本研究で得られた台風の発生・進路予測に関する成果は、予測の不確実性の把握と利活用に資する有用な知見となり、台風の理解を深めるとともに台風防災に貢献するものである。
謝辞
本研究を進めるにあたり、主査である横浜国立大学の筆保弘徳教授、副査である横浜国立大学の下出信次教授、横浜国立大学の吉田龍二准教授、名古屋大学の坪木和久教授、東京大学の佐藤正樹教授には本論文を審査いただき、厚く御礼申し上げます。
また、共同研究者である気象庁気象研究所の山口宗彦主任研究官および嶋田宇大主任研究官、横浜国立大学の筆保弘徳教授および吉田龍二准教授には多大なるご指導を賜り、深く感謝申し上げます。
引用文献
- Ito, K., C.-C. Wu, K. T. F. Chan, R. Toumi, and C. Davis, 2020: Recent progress in the fundamental understanding of tropical cyclone motion. J. Meteor. Soc. Japan, 98, 5–17.
- Nishimura, S., M. Sasaki, N. Nonaka, M. Ueno, Y. Mochizuki, and M. Miura, 2023: The Japan Meteorological Agency's Dvorak re-analysis data. RSMC Tokyo – Typhoon Center Technical Review, 26, 1–12.
- Ritchie, E. A., and G. J. Holland, 1999: Large-scale patterns associated with tropical cyclogenesis in the western Pacific. Mon. Wea. Rev., 127, 2027–2043.
- Yamaguchi, M., F. Vitart, S. T. K. Lang, L. Magnusson, R. L. Elsberry, G. Elliott, M. Kyouda, and T. Nakazawa, 2015: Global distribution on the skill of tropical cyclone activity forecasts from short- to medium-range time scales. Wea. Forecasting, 30, 1695–1709.
- Yoshida, R., and H. Ishikawa, 2013: Environmental factors contributing to tropical cyclone genesis over the western North Pacific. Mon. Wea. Rev., 141, 451–467.
- Yoshida, R., and H. Fudeyasu, 2020: How significant are low-level flow patterns in tropical cyclone genesis over the western North Pacific? Mon. Wea. Rev., 148, 559–576.
Copyright © 2025 Yasuhiro Kawabata. All rights reserved.